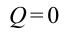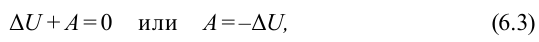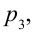что значит адиабатный процесс
Адиабатный процесс, его суть и и формулы
Связь с первым началом термодинамики
Адиабатный процесс (адиабатический) можно напрямую связать с первым законом термодинамики. Его формулировка “по умолчанию” звучит следующим образом: изменение количества теплоты в системе при протекании в ней термодинамического процесса будет численно равно сумме изменения внутренней энергии идеального газа и работы, совершаемой этим газом.
Если мы попытаемся записать первое начало термодинамики в его стандартном виде, то получим следующее выражение: dQ = dU + dA. А теперь постараемся видоизменить эту формулу применительно к адиабатическому процессу. Как было сказано ранее, подобные процессы протекают при условии отсутствия теплообмена с окружающей (внешней, как ее называют некоторые литературные источники) средой.
Следствие из первого начала термодинамики для адиабатического процесса
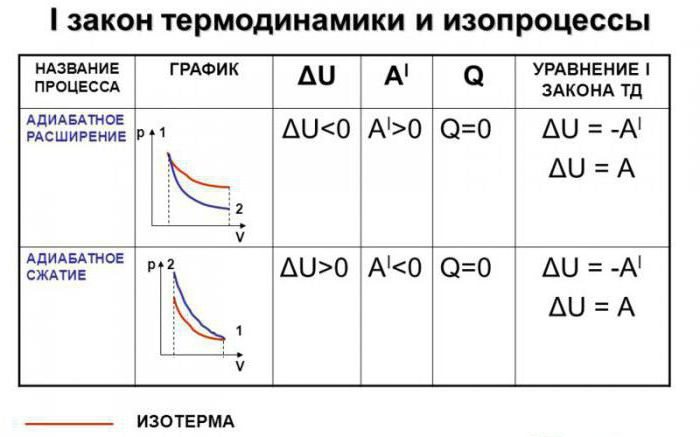
Допустим, что в системе произошел адиабатный процесс. В этом случае можно, не вдаваясь в мельчайшие детали, говорить о том, что газ при расширении совершает работу, но при этом он теряет свою внутреннюю энергию. Иными словами, работа, совершаемая при адиабатном расширении газа, будет осуществляться за счет убыли внутренней энергии. Следовательно, в качестве исхода этого процесса мы будем рассматривать понижение температуры самого вещества.
Абсолютно логично можно предположить, что если газ будет адиабатически сжат, его температура вырастет. Несложно заметить, что в ходе процесса будут изменяться все главные характеристики идеального газа. Речь идет о его давлении, объеме и температуре. Следовательно, грубой ошибкой стало название адиабатического процесса изопроцессом.
Адиабатный процесс. Формулы
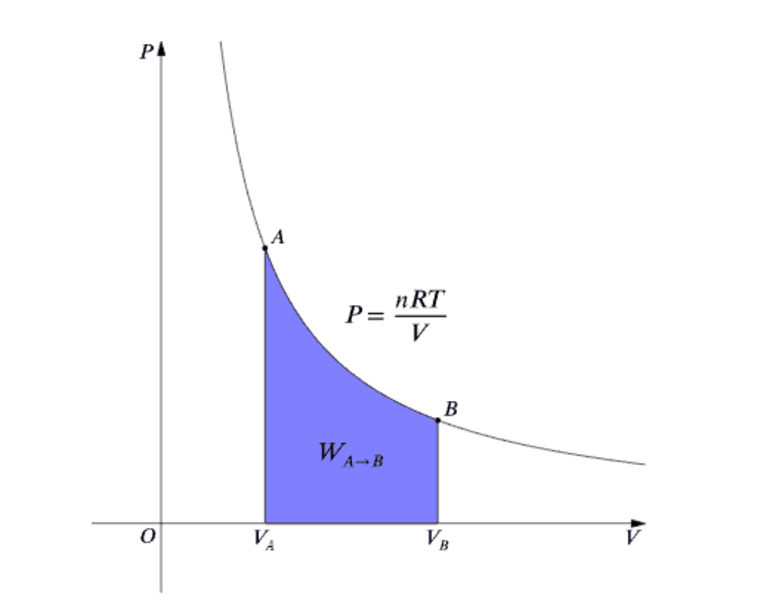
Ранее была записана формула, выведенная из первого начала термодинамики. Используя ее, мы без особого труда можем вычислить работу в общем виде, которую будет выполнять газ при течении адиабатного процесса. Как вы уже могли догадаться, делать это мы будет при помощи интегрирования.
Уравнение адиабаты
Используя первое начало термодинамики для адиабатного процесса, мы можем найти уравнение адиабаты. При этом оно будет записано для произвольного числа молей идеального газа. Итак, запишем первоначальную формулу. Она имеет такой вид: dA + dU = 0. Но ведь мы прекрасно знаем, что работа идеального газа представляет численно собой не что иное, как произведение давления на изменение объема.
В то же время изменение внутренней энергии будет равно работе, взятой с обратным знаком. А ее-то мы уже нашли при помощи интегрирования. Значит, первое начало термодинамики для адиабатического процесса может принять следующий вид: pdV + xCvdT = 0. Из этого уравнения нам нужно исключить один показатель, а именно, температуру. Вернее, ее изменения. Чтобы сделать это, мы обратимся к достаточно часто используемому в молекулярной физики уравнению. А именно к уравнению Менделеева-Клапейрона.
Первичное выражение
По сути дела, первая часть задачи выполнена. Остается только довести все до ума.
Вторичное выражение. Подстановка значения
Возьмем полученную в результате дифференцирования формулу Менделеева-Клапейрона и подставим ее в выражение, выведенное нами ранее для первого закона термодинамики по отношению к адиабатному процессу. Итак, что мы получим? Все это громоздкое выражение примет следующий вид: pdV + xCv ((pdV + Vdp)/x(Cp-Cv)) = 0.
Чтобы упростить все это, мы должны принять во внимание пару фактов. Во-первых, упростить выражение можно за счет приведения к общему знаменателю. Когда мы получим одну дробь, мы можем воспользоваться старым добрым правилом, которое гласит, что дробь равна нулю, когда ее числитель равен нулю, а знаменатель от нуля отличен. В результате совокупности всех этих действий мы получим следующее выражение: pCpdV – pCvdV + pCvdV + VCvdp = 0.
Теперь следующим шагом мы можем разделить данное выражение на pVCv. Получим сумму двух частей, дающих в итоге ноль. Это будет Cp/Cv * dV/V + dp/p = 0. Эту формулу необходимо проинтегрировать. Тогда мы получим следующее выражение: y (интеграл) dV/V + (интеграл) dp/p = (интеграл) 0.
Ну а дальше все достаточно просто. Воспользовавшись формулами интегрирования (можно использовать табличные интегралы, чтобы все было проще), получим в итоге следующую запись: y ln V + ln p = ln (const). Получается, что p(V)y = const. Данное выражение называется в молекулярной физике уравнением Пуассона. Многие литературные источники научной направленности также называют эту формулу уравнением адиабаты. В то же время величина y, которая имеет место в данной записи, называется показателем адиабаты. Она равна (i+2)/i. Нужно отметить, что показатель адиабаты всегда больше единицы, что, в принципе, логично.
Примеры адиабатных процессов
Вскоре после того, как был открыт адиабатический процесс, стартовало огромное количество различных исследований. Так, была создана первая теоретическая модель, имеющая отношение к циклу Карно. Именно она позволила установить условные пределы, ограничивавшие развитие тепловых машин. Но в случае некоторых реальных процессов осуществлять цикл Карно достаточно трудно. Все дело в том, что в его состав входят изотермы. А они, в свою очередь, требуют задания определенной скорости термодинамических процессов.
Заключение
С целью обойти подобные проблемы был придуман цикл Отто, а также цикл сжижения газа. Они стали широко применяться при решении конкретных задач на практике. Стартовавшие исследования показали возможность описания некоторых природных процессов в адиабатическом плане, что позволило выявлять общие закономерности соответствующих процессов. Примером адиабатического процесса можно смело назвать химическую реакцию, которая происходит внутри некоторого объема газа, если система является замкнутой, а обмен с внешней средой теплом отсутствует.
История открытия
Ряд экспериментов, проведенных в начале XIX столетия, доказали существование атмосферного давления. Так, немецкий инженер Герике сконструировал магдебургские полушария. Из сферы выкачивался воздух, после чего они с трудом разъединялись — воздух давил на них.
Пример еще одного исследования, целью какого является изучение такого явления — опыт Роберта Бойля. Физик доказал, что если трубка запаяна с короткого конца, а в длинный налита ртуть, последняя не поднимется до верха. Ведь воздушными потоками уравновешивается давящая сила.
Ламберт издал в 1779 году книгу «Пирометрия». В его труде описывается повышение и понижение температуры в приемнике воздушного насоса, когда движется поршень. Этот эффект подтвердили следующие ученые:
Дальтон опубликовал доклад, где называется особенность сгущения идеального газа. При нем выделяется тепло.
Обобщил накопившиеся знания Пуассон. По его мнению, температура при адиабатической реакции непостоянная, а, значит, закону Бойля — Мариотта необходима поправка — физик обозначил ее, как коэффициент k и выразил через соотношение теплоемкостей.
Важные нюансы
Термодинамический процесс в общем случае включает в себя теплообмен, работу, совершаемую системой и изменение внутренней энергии. Адиабатный по причине отсутствия обмена теплом сводится к последним двум.
Энтропия (S) не меняется в результате теплопередачи. Этот постулат описывается уравнением ΔS = ΔT=0. Здесь T — температура.
А также для расчетов используется такая величина, как адиабата идеального газа. Она обозначается буквой γ и вычисляется следующим образом: γ = C1/C2 (соотношение теплоемкостей).
Может подобный параметр выражаться и как количество степеней свободы. То есть γ = i + 2/ i.
Описание основных циклов
Физиками предлагается указанное определение процесса Карно: это идеальная цикличность, обеспечивающая работу тепловой машины с максимальным КПД. Наибольший и наименьший уровень разогрева совпадает с аналогичными показателями для рабочего устройства.
Среди условий для достижения нужного коэффициента полезного действия физики называют обратимость реакции, значит, следует исключить теплообмен между телами. Соответственно, преобразование тепла происходит лишь изотермически.
Обратный переход рабочего двигателя в исходную точку невозможен. Дело в том, что вся энергия затратится на восстановление изначального положения.
Работа четырехтактной двигательной системы осуществляется по схеме Отто, включающую в себя впуск, сжатие, рабочий вход и выпуск. Второй, третий и четвертый этапы считаются адиабатическими.
Прилагаемые в конце усилия равны разности мощности, с которой давят на газ и силы, затраченной на сжимание. Последнее повторяется до 7 раз (применяемая смесь зажигается принудительно).
Особенность адиабатической реакции заключается в невозможности теплообмена между окружающим пространством и объектом. С ее помощью можно объяснить, каким принципам подчиняется работа двигателя с четырьмя тактами и устройство с высокой отдачей.
Адиабатный процесс

Всего получено оценок: 64.
Всего получено оценок: 64.
Среди различных явлений, происходящих с газами, важную роль играет адиабатный процесс. Он широко используется в технике и часто встречается в Природе. Рассмотрим его суть более подробно.
Адиабатный процесс
При изучении законов газовых процессов (изопроцессов) для изменения внутренней энергии газа используется обмен теплом с внешними источниками. Например, в изохорическом процессе, когда объем газа не меняется, увеличение внутренней его энергии возможно за счет внешнего нагрева. Обмен теплом также происходит и в изобарическом и изотермическом процессах.
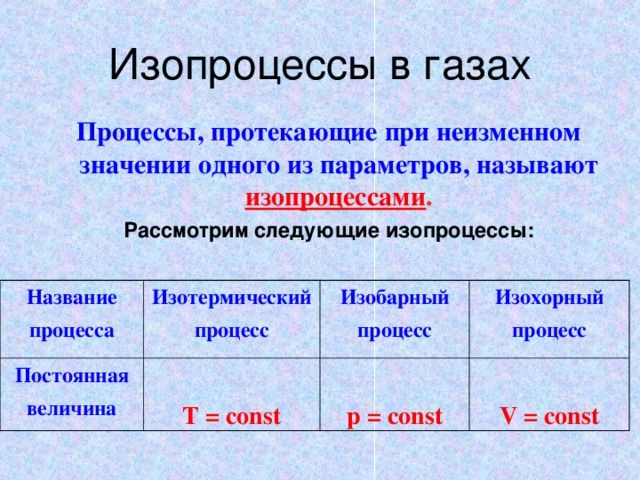
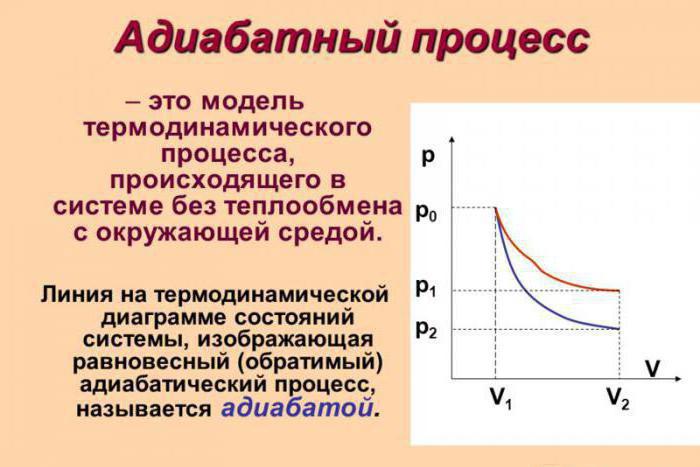
Однако, состояние газа и его внутренняя энергия могут меняться и без теплового обмена с внешними источниками. Такой процесс, для которого количество подведенного тепла равно нулю ($Q=0$), называется адиабатным.
Для того, чтобы газовый процесс был приближен к адиабатному в реальных условиях, существует два способа (и их комбинация). Во-первых, можно окружить систему толстой теплоизолирующей оболочкой, сильно замедляющей обмен теплом. Во-вторых, процесс можно проводить очень быстро, при этом теплообмен просто не успеет произойти.
На первый взгляд, может показаться, что если к системе не подводится тепло, то она не может совершать работу. Однако, это не так. Согласно Первому Закону термодинамики, изменение внутренней энергии системы равно сумме работы внешних сил и количества тепла переданного системе:
А это значит, что в адиабатном процессе совершение работы возможно. Но вся эта работа будет произведена за счет изменения внутренней энергии газа.
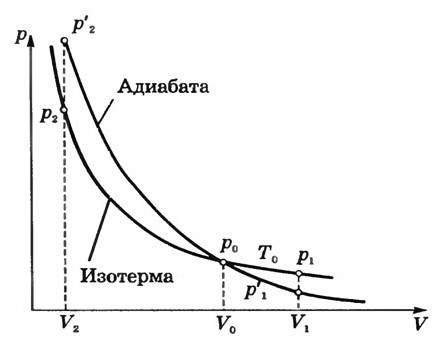
График адиабаты
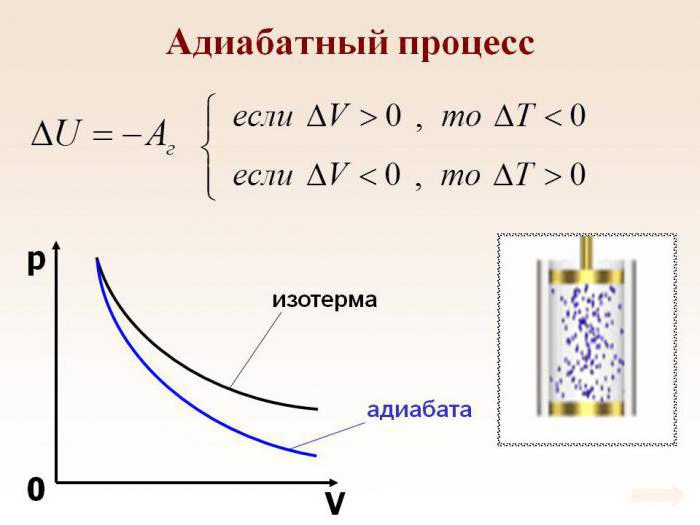
Характеристикой внутренней энергии газа является его температура. То есть, если в адиабатном процессе производится работа, то это происходит с обязательным изменением температуры. Например, если работа положительна, и внешние силы сжимают газ, то его температура увеличится, газ нагреется.
Можно вывести математические уравнения данных процессов:
Показатель
Адиабатные процессы в Природе и технике
Поскольку при быстром сжатии и расширении газа теплообмен очень невелик, адиабатные процессы широко используются в технике, и играют большую роль в атмосферных явлениях в Природе.
Например, в двигателях внутреннего сгорания горючая смесь после впуска в цилиндр в течение короткого времени сжимается, а затем, после воспламенения смеси в течении короткого времени расширяется. Таким образом, такты сжатия и рабочего хода в двигателях являются хорошими примерами адиабатного процесса.
Значительный нагрев газа при адиабатном процессе используется в дизельных двигателях. В этих двигателях нет систем для поджигания сжатой топливовоздушной смеси. В дизеле происходит сжатие атмосферного воздуха, сильнее, чем в бензиновом карбюраторном двигателе. А в конце сжатия топливо впрыскивается в цилиндр с помощью специальной форсунки. В этот момент воздух имеет температуру, достаточную для самовоспламенения впрыснутой горючей смеси, температура сгоревшей топливовоздушной смеси резко возрастает, смесь расширяется, толкая поршень и совершая полезную работу.
Природные адиабатные процессы играют значительную роль в формировании погоды. Нагретые массы воздуха быстро поднимаются вверх и расширяются. В результате их температура падает ниже точки росы, и влага, содержащаяся в воздухе, конденсируется в облака. Однако, при снижении снова происходит адиабатное сжатие, температура повышается, и облачные капли у нижней границы облаков снова превращаются в пар.
Что мы узнали?
Адиабатический процесс:
Процесс, который происходит без обмена тепловой энергии с окружающей средой, называется адиабатическим процессом.
Примерами адиабатического процесса могут служить процессы, которые происходят быстро. Например, выполненная работа при быстром сжатии газа приводит к росту его температуры, т.е. внутренней энергии. Для распространения тепла в окружающую среду в результате повышения температуры требуется определенное время. Поэтому
Горение горючей смеси в двигателе внутреннего сгорания является примером адиабатического процесса.
Для адиабатического процесса первый закон термодинамики имеет следующий вид:
т.е. в адиабатическом процессе работа выполняется за счет изменения внутренней энергии.
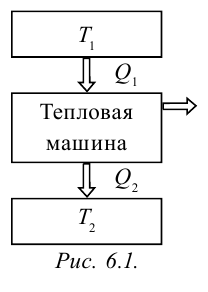
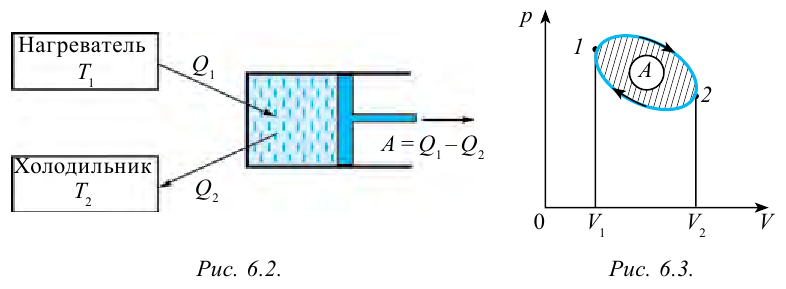
Тепловыми машинами называют машины, которые превращают внутреннюю энергию горючего в механическую энергию.
Принцип работы тепловой машины показан на рисунке 6.1. За один цикл нагреватель с температурой 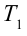
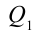
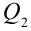
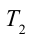
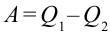
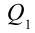
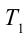
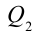
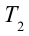
циклически.
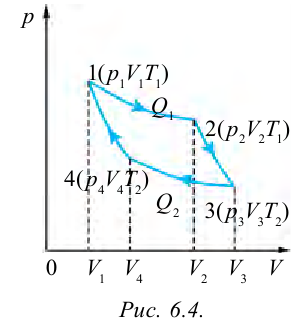
Круговым процессом или циклом называется процесс, в котором система проходит через несколько состояний и возвращается в начальное состояние (рис. 6.3). Процесс, который происходит по направлению часовой стрелки (газ сначала расширяется, затем сжимается) называется правильным циклом, процесс, который происходит против часовой стрелки (газ сначала сжимается, затем расширяется) называется обратным циклом. Тепловые машины работают на основе правильного цикла, а холодильники работают на основе обратного цикла. Когда цикл завершается, рабочее вещество возвращается в свое первоначальное состояние, т.е. его внутренняя энергия равна начальному значению.
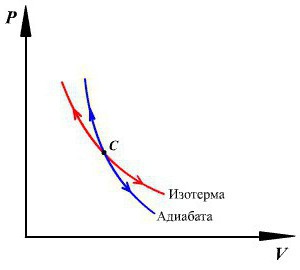
Цикл Карно – это обратимый круговой тепловой процесс, который состоит из последовательно взаимно меняющихся двух изотермических и двух адиабатических процессов (рис. 6.4).
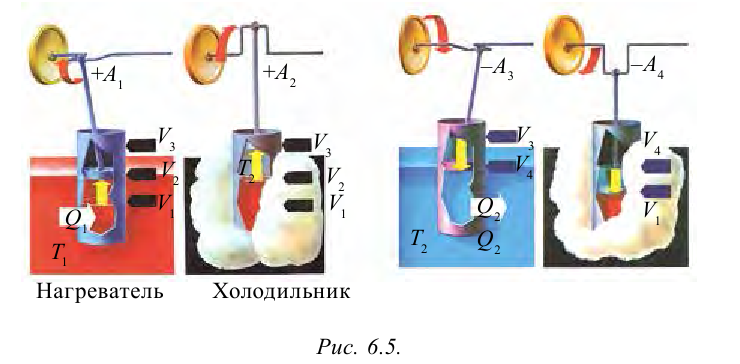
Рассмотрим на примере поршневого цилиндра с коленчатым валом и шатуном (рис. 6.5) цикл, который состоит из двух изотермических и двух адиабатических процессов, так называемый цикл Карно.
1. На самом нижнем уровне поршня в цилиндре объем газа равен 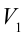
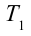
будет 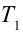
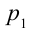
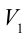
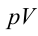
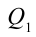
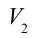
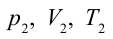
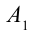
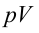
2. На второй адиабатической стадии расширения, несмотря на уменьшение количества тепла 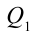
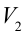
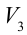
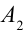
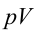
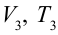
3. Для совершения изотермического сжатия газа цилиндр с температурой 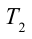
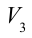
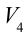
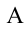
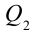
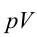
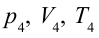
4. В последней части цикла газ адиабатически сжимается, поршень уменьшает объем газа с 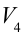
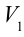
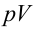
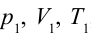
Таким образом, идеальный газ возвращается в свое начальное состояние и полностью восстанавливает свою внутреннюю энергию. В течение цикла идеальный газ от нагревателя забирает количество тепла 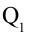
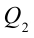
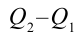
Коэффициент полезного действия тепловой машины:
Коэффициентом полезного действия тепловой машины или цикла Карно называется следующая величина:
Если учесть работу, выполненную тепловой машиной, т.е. 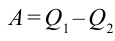
Также КПД цикла Карно можно выразить через температуру нагревателя 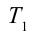
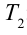
Значит, КПД идеальной тепловой машины не зависит от вида рабочего вещества и определяется только температурами нагревателя и охладителя.
Из выражения (6.6) можно сделать следующие выводы:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.